In this unit students explore patterns and relationships among the circle numbers and box numbers that form different arithmagons. Students identify, and use rule-based patterns, and linear equations to solve a range of arithmagons, beginning with square and triangular arithmagons. They establish and prove algebraically the general rules for solving arithmagons.
- Devise rules based on numerical patterns to solve triangular arithmagons.
- Explain the condition for the solution of any square arithmagon.
- Form and use linear equations to solve triangular arithmagons.
- Develop proofs of rules and conditions for the solution of arithmagons.
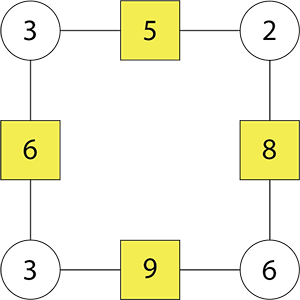
This unit is based around exploring ‘arithmagons’. Arithmagons are polygons with a circle number on each vertex, with a number inside each of those circles (circle numbers). Each side of the arithmagons includes a box with a number inside of it (box numbers). Each box number is the sum of the two circle numbers adjacent to it.
Notice, in the example below, that the two circle numbers at the corners of a side add up to the box number in the middle of that side. For example, 2 + 3 = 5 and 3 + 3 = 6.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- working with calculators to reduce the cognitive load associated with calculation and promote a focus on generalisations
- providing multiple examples of problems with numbers before using algebra to solve the problems
- using materials (e.g. counters, number lines, digital diagrams) to model creating and solving arithmagons with smaller numbers
- developing students’ capacity to manipulate linear expressions.
The context for this unit is a mathematical puzzle in the form of polygons. Motivate students to attempt the problems by creating a context, such as an adventure, which appeals to and engages your students. You could set up the class with hidden arithmagons and clues. Each successfully solved arithmagon could lead students to an area of the room with more hidden arithmagons. With a little extra preparation, the answers to the arithmagons could also be used as the solution to a simple word puzzle (e.g. an anagram, code breaker). Students often encounter similar cognitive challenges when playing video games.
Alternatively, you could choose contexts that are culturally-relevant, or that reflect students’ interests and learning from other curriculum areas, to frame each new arithmagon session in. Exploration of these mathematical puzzles could also motivate students to research other mathematical puzzles. Perhaps they have mathematical puzzles or riddles at home which they could share with the class.
Te reo Māori kupu such as tapatoru (triangle), tapawhā rite (square), taparima (pentagon), tapaono (hexagon), tapawhitu (heptapgon), tapawaru (octagon), ture (rule, formula), and kīanga taurangi (algebraic expression) could be introduced in this unit and used throughout other mathematical learning.
Note that Copymasters 1 - 5 could be collated onto a PowerPoint and presented digitally to the class.
- Copymaster 1 (triangular arithmagons)
- Copymaster 2 (square arithmagons)
- Copymaster 3 (pentagonal arithmagons)
- Copymaster 4 (hexagonal arithmagons)
- Copymaster 5 (heptagonal and octagonal arithmagons)
- Resources to create a class chart
Each session in this unit comprises a sequence of tasks or challenges. It is suggested that students have an opportunity to engage in each task by themselves, or with a peer, before they begin sharing their ideas with other students or with their teacher. Encourage students to explain and justify their thinking to others. The unit provides multiple opportunities for posing and testing conjectures, and using algebra to prove whether or not the conjectures hold.
Session 1
In this session, students are likely to use a ‘trial and improvement’ strategy to find circle numbers. Encourage students to look for shortcuts (or the most efficient methods) that result in correct solutions. The tasks are designed to draw students’ attention to sets of box numbers for which the shortcut works and doesn’t work. Identifying arithmagons that can be solved but for which the short cut doesn’t work can encourage further exploration into new and more robust short cut methods. Begin by introducing students to the rules for arithmagons, ie. that each box number is the sum of the two circle numbers adjacent to it.
In this introductory session, students should be provided with plenty of explicit teaching in order to fully understand this new concept of arithmagons. They should also have ample opportunities for collaborative thinking (mahi-tahi) and peer-support (tuakana-teina)
- Look carefully at the completed triangular arithmagon below.
What do you notice? (The numbers in boxes are the sum of the circle numbers on that side).
Complete the second triangular arithmagon by putting numbers in the circles.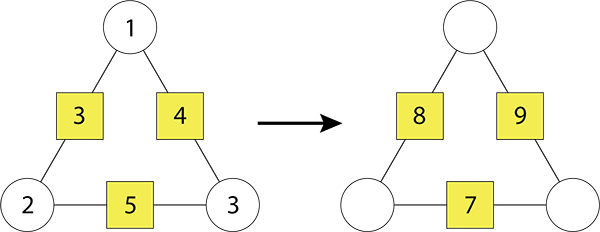
- Model calculating the sum of each box number in the completed arithmagon.
I’m going to add 1 and 2 to create 3 - the sum.
Do you notice anything about the numbers in the circles and in the squares? Students may notice that the numbers are consecutive. - Have students work in pairs, small groups, or independently to complete the second triangular arithmagon.
Complete the second triangular arithmagon by putting numbers in the circles.
Remember to write the sum - the number that is created when the numbers are added together. - Discuss the strategies students used to solve the problem.
Most may use trial and error with some sense of reasonable numbers to include. Some may realise that the circle numbers must be different and possibly that they are consecutive. The numbers in the boxes give a sense of the relative size of the circle numbers.
For example, 9 = 4 + 5. Which circle will five go in? Why? (At the top since eight and nine are the largest side totals). - Pose the following problems that are sufficiently hard to make non-trial and error strategies productive.
Find the circle numbers for these arithmagons.
Show how you know that your circle numbers are correct.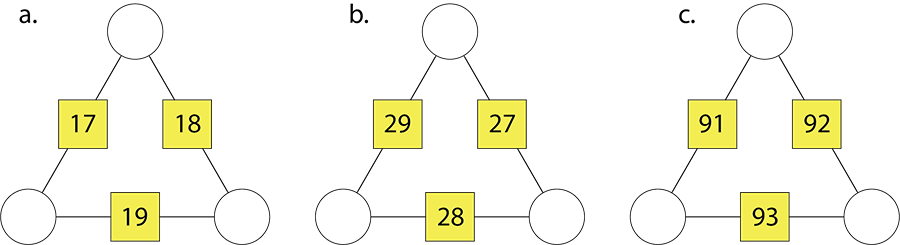
Answers: a. 8, 9, 10 b. 13, 14, 15 c. 45, 46, 47 - Pose this problem:
Jenny uses these arithmagons to show her rule for working out circle numbers. Show how Jenny’s rule works.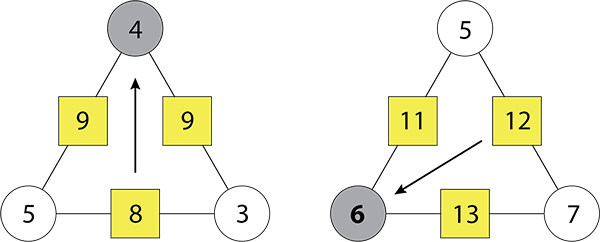
Ask students to discuss what they believe Jenny is doing and why the rule works. - Share what students notice.
E.g. Jenny finds the middle box number and halves it to get the circle number that is opposite. For example, she halves eight to get four. Then she works out the other two circle numbers that are always one more and one less than the first circle.
What does the half number Jenny finds have to do with the sum (total) of the box numbers?
For the left arithmagon the sum of circle equals 24 which is six times the circle number Jenny finds. That also works for the right arithmagon as well. - Have students check that Jenny’s rule works for the following arithmagons.
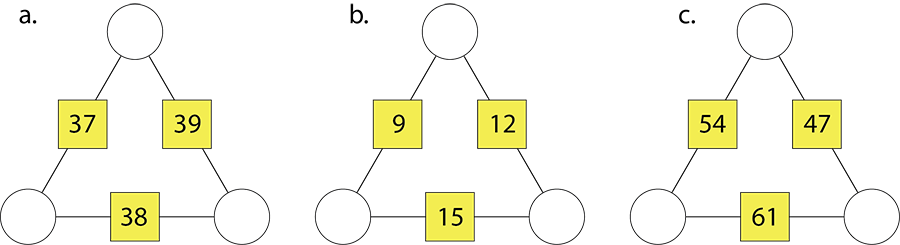
Students should notice Jenny’s rule works for all three arithmagons. Answers : a (18, 19, 20), b (3, 6, 9), c (20, 27, 34). It is important that Jenny starts with the box number that is the middle of the three numbers. For arithmagon b), Jenny would start with 12 because it lies between 9 and 15 on a number line).
Is there something the same about all three arithmagons that mean Jenny’s rule will work?
Students might notice that there is a constant difference between the box numbers in each arithmagon. For example, 9, 12, 15 are different by three and 47, 54, and 61 are different by seven. - Will Jenny’s rule work on all arithmagons?
Decide if Jenny’s rule works for each of these arithmagons.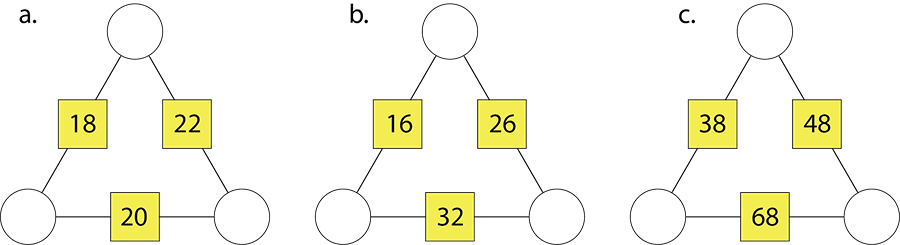
Jenny’s rule works for the left arithmagon but doesn’t work for the other two examples.
What is different about the arithmagons that do not follow Jenny’s rule? - Use your own three box numbers to make an arithmagon (Copymaster 1) that can be solved using Jenny’s rule. Allow students, as necessary, to work on this with a partner, in small groups, independently, or in a teacher-guided group.
- Make an arithmagon that cannot be solved using Jenny’s rule. Explain why it cannot be solved in this way.
- Review the arithmagons created by students by having students share their work with a peer, and then having a few share their work with the class. End the session by reviewing the different facts students have learnt about arithmagons. These facts could be added to a class chart for future reference.
Session 2
In this session students work towards creating a general rule for solving triangular arithmagons.
- Review the key learning from the first session.
What do you remember about arithmagons?
Look for students to identify that each box number is the sum of the two circle numbers adjacent to it, that the numbers in the squares and circles are consecutive, and to recall Jenny’s rule. If you created a class chart of these facts at the end of the last session, then this could be used to remind students of the key learning. - Introduce the aim of the session and draw students’ attention to the following arithmagons.
We are trying to find a way to solve any triangular arithmagon. Jenny’s rule only works for some cases.
Look at these arithmagons.
What is the relationship between the blue number and the three box numbers?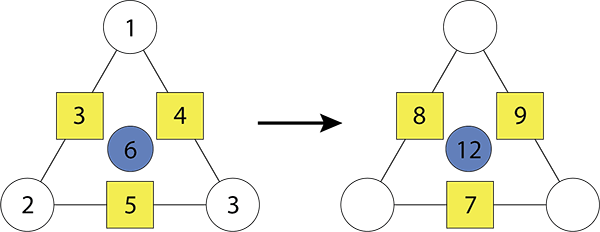
Students should notice that the blue number is half the sum of the box numbers. Or example, in the left arithmagon 3 + 4 +5 = 12 and 12 ÷2 = 6.
- Look at the left triangular arithmagon that has the circle numbers filled in.
How might knowing the blue (centre) number help you to find the other circle numbers?
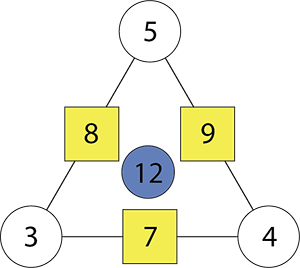
Students should notice that the opposite box and (white) circle numbers add to the blue number. - Apply this thinking to highlight the relationship between each of the numbers in the left arithmagon. For example, 2 + 4 = 6 and 3 + 3 = 6 and 1 + 5 = 6.
- Have students apply this thinking solve the right arithmagon. Following that rule gives this solution:
Give the students these arithmagons without the blue number. Have them work on the arithmagons in appropriate groupings, and provide support to ensure they apply the discussed rules.
Find the blue numbers for these arithmagons then find the circle numbers.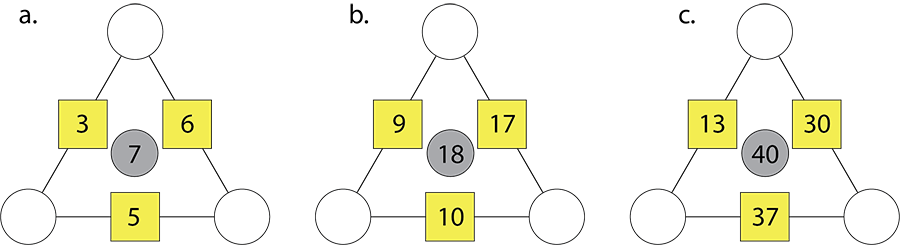
Share students’ solutions. Draw attention to the relationships between the numbers and the application of the thinking that the opposite box and white circle numbers add to the blue (centre) number.
- Extend the use of the blue number to these more difficult arithmagons:
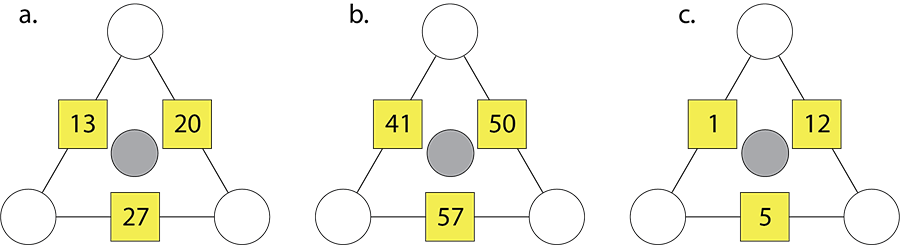
- Try to develop a generalisation for why using the blue number works.
Imagine a triangular arithmagon with any three numbers in the circles. Let’s call the numbers a, b, and c. Draw this diagram.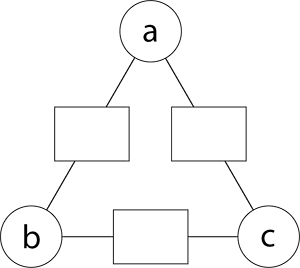
What are the box numbers for this arithmagon?
Students might comment that it depends on a, b, and c.
That is true but we can still write an expression for each box number. - What did you do with a, b, and c to get the box numbers in the previous task? (Added a + b, b + c, and a + c)
Add to the diagram as below: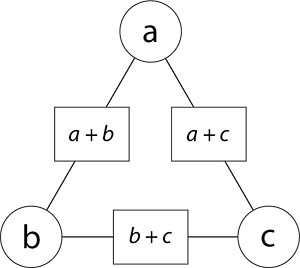
- Ask students to write an expression for the blue number and add it to their diagram. They might record (a + b + b + c + a + c) ÷
2 which is correct,
It looks like you have two of all three numbers, a, b and c.
Can you write the blue number in a simpler way? (a + b + c)
Add the blue number to the diagram.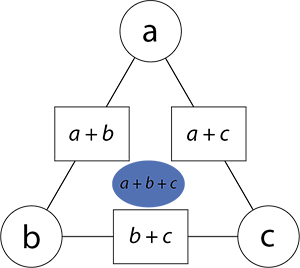
What do you notice?
Students might see that joining opposite circle numbers and box numbers always results in a + b + c.
They might also notice that if the circle numbers were not known they could find them from the circle numbers and the blue numbers. For example, subtracting the left box number from the blue number gives the number in the right circle. That is because a + b + c – (a + b) = c.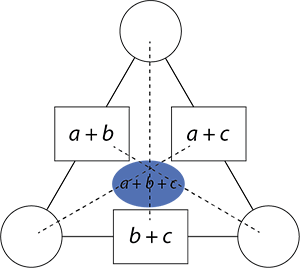
- Write a rule that can be used to work out any circle number, a, b or c, for any triangular arithmagon. (Blue number – opposite box number)
- Ask students to create a triangular arithmagon for a classmate to solve, such as those below. Following this, students who have succesfully grapsed all ideas could work on one of the extensions described below. For students who have not yet grasped the idea of these generalisations, consider running a small group teaching session to reinforce the concepts covered throughout this session.
Extensions
- Make a triangular arithmagon, (Copymaster 1), that has one box number the same as the centre number.
- What do you notice?
- Make up several different triangular arithmagons that have one box number the same as the centre number.
- Write a rule that tells you if a triangular arithmagon has one box number that is zero. Check that your rule always works by making your own triangular arithmagons.
- Make a triangular arithmagon (Copymaster 1) that has a box number greater than the centre number.
- What do you notice?
- Write a rule that tells you if an arithmagon has a circle number that is less than zero.
- Make up several different triangular arithmagons that have one box number greater than the centre number. Check that your rule works.
Session 3
In this session the problems are extended to square arithmagons. These arithmagons all have multiple solutions – in fact, whenever a square arithmagon can be solved, there is an infinite number of solutions when negative or fractional values are permitted.
- Find the missing circle numbers for these square arithmagons. One circle number in each arithmagon is shown.
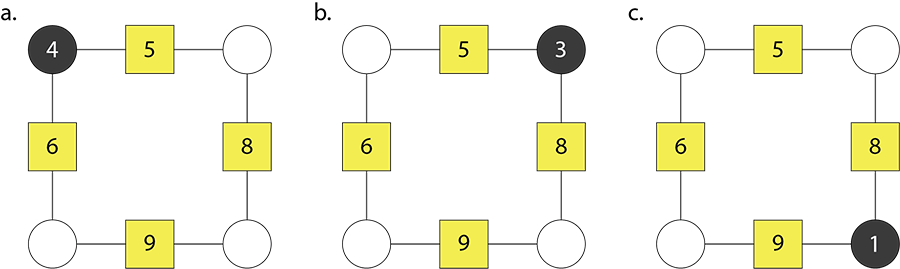
Students will realise that setting the black circle number dictates the size of the other circle numbers. - Make three more square arithmagons, (Copymaster 2), that have the same box numbers as in Question 1. For example, here are other solutions for the left arithmagon.
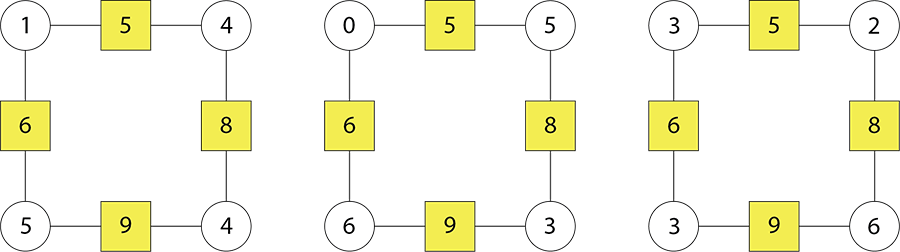
If you change the black circle number, can you still find a solution? Play with one example and find as many solutions as you can. - How many different square arithmagons do you think can be made with the box numbers as above? Explain your reasoning. Prompt students to consider using fractions and negative integers as appropriate to their level of knowledge
Do students realise that integers like -3 and -7 could be used in the circles?
Do students realise that fractions like 3 ½ and 5 ¼ could be used in the circles? - Provide students with the following arithmagons to work on in pairs or small groups.
Not all square arithmagons are solvable. Decide which square arithmagons below can be solved and which ones cannot.
Discuss which arithmagons were solvable and which were not.
Is there something in common with the solvable arithmagons? (Opposite squares add to the same total)
Is there something in common with the unsolvable arithmagons? (Opposite squares do not add to the same total) - Pose this problem:
Val changes the box number 6 to 4. She claims that the new square arithmagon can now be solved. Check to see if she is correct.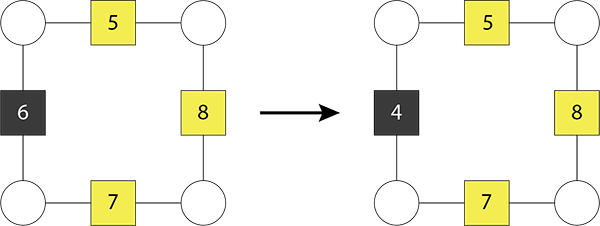
Discuss why Val’s method works. Changing the six to four means that both pairs of opposite box numbers add to 12. - For any arithmagon in Question 1 that cannot be solved, change just one box number so that the new arithmagon can be solved.
- Write a rule that tells whether square arithmagons can be solved.
Session 4
In this session, students have an opportunity to work with algebraic symbols to formulate and solve linear equations and to prove results for triangular arithmagons. Notice that rather than using algebraic symbols, such as x and y, for box numbers or circle numbers, it is likely to be more helpful to use b1, b2 and b3 etc., to represent successive box numbers and c1, c2 and c3 etc., to represent successive circle numbers. Students may need support to understand how this system of subscript symbols work.
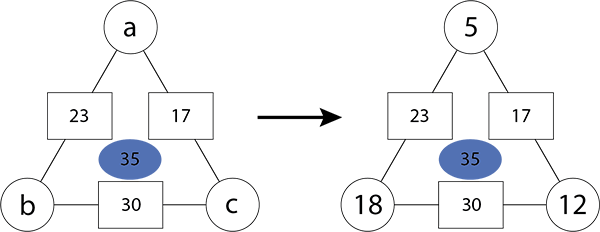
- Maraea starts with the arithmagon on the left and then puts 25 – a for one circle number and 17 – a for the other. Show how Maraea worked out these algebraic expressions.
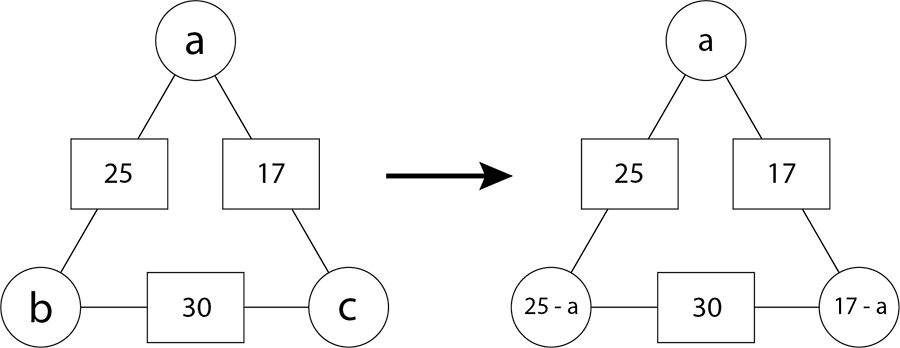
- Maraea wrote the equation, 42 – 2a = 30 for her arithmagon.
- Show how she got this equation and then solve it to find the value for C1.
- Find the values for the three circle numbers in Maraea’s arithmagon.
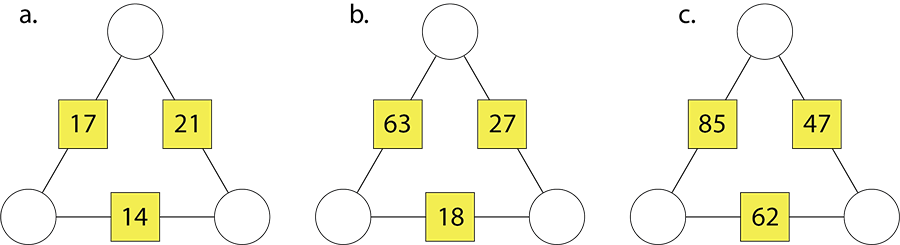
- Use algebra to solve the following triangular arithmagons.
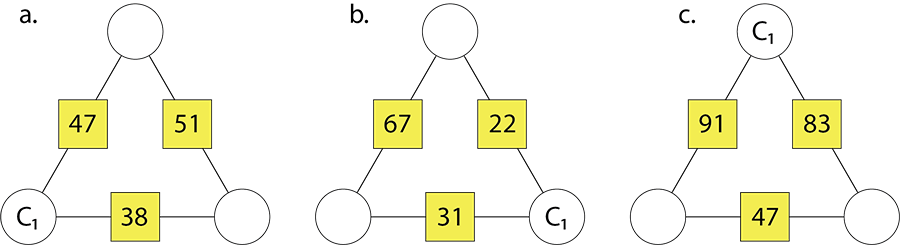
- Use algebra to find the three circle numbers for each of the following arithmagons.
- Make up three triangular arithmagons with your own box numbers (use any numbers including negative numbers).
- Give your arithmagons to a partner. Ask them to use algebra to find the circle numbers.
Session 5
In this session, students extend their algebraic work to square, pentagonal, hexagonal, heptagonal, and octagonal arithmagons. They examine the generality of solutions for arithmagons. Consider integrating opportunities for peer work and small-group, explicit teaching to ensure the concepts covered are accessible to all.
- Show how Albert got the algebraic expressions, 8 – a and 7 – a for circle numbers b and d in this arithmagon.
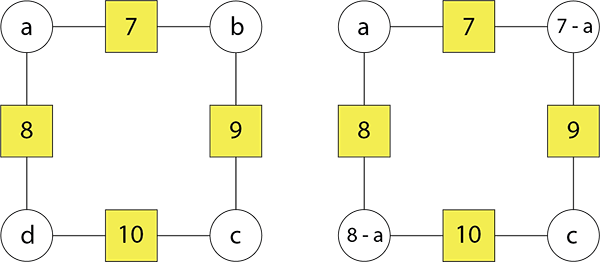
What expression can Albert write for circle number c?
Can you find another expression for c?
Students might find that 10 – (8 – a) and 9 – (7 – a) are both names for c.
We can write 10 – (8 – a) = 9 – (7 – a). Explain why we can use the equal sign. - Use Albert’s rule to find the value of c when given a.
For example, start with a = 6. Does that work?
If a = 6 then c = 10 – (8 -a) = 10 – (8 – 6) = 8 or c = 9 – (7 – a) = 9 – (7 – 6) = 8.
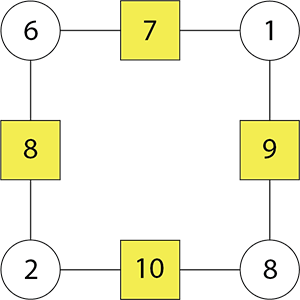
Now you know a = 6 and c = 8, work out b and d.
If a = 6 then b = 7 – a = 7 – 6 = 1 and d = 8 – a = 8 – 6 = 2. - Check to see the arithmagon works:
- Make up three square arithmagons with your own box numbers. (Use any numbers including negative numbers but make sure you choose numbers that allow the arithmagon to have a solution.
- For extension, use an algebraic rule to find circle numbers that work for the pentagonal arithmagon. Take the example below:
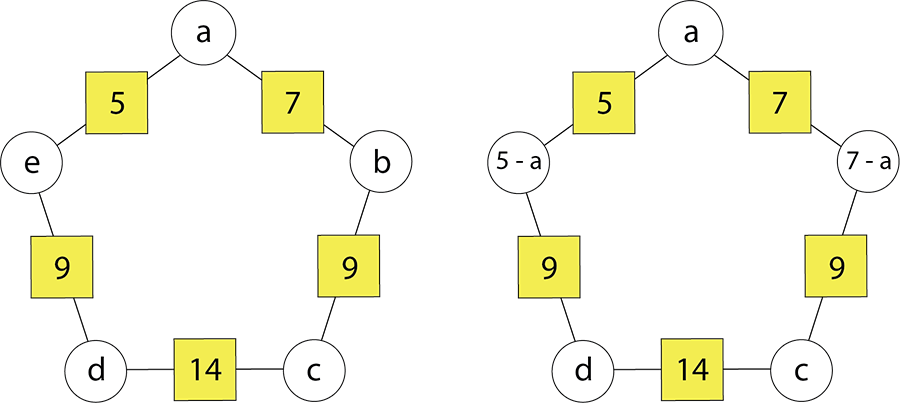
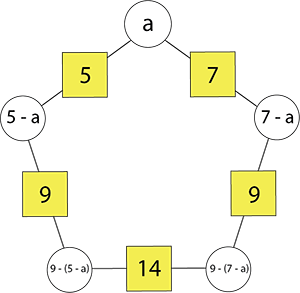
Combining the expressions for c and d we get 9 – (5 – a) + 9 – (7 - a) = 14. Solve the equation:
9 – (5 – a) + 9 – (7 - a) = 14
9 – 5 + a + 9 – 7 + a = 14
6 + 2a = 14
2a = 8
a = 4
Use a = 4 to solve the arithmagon.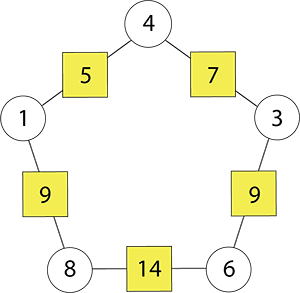
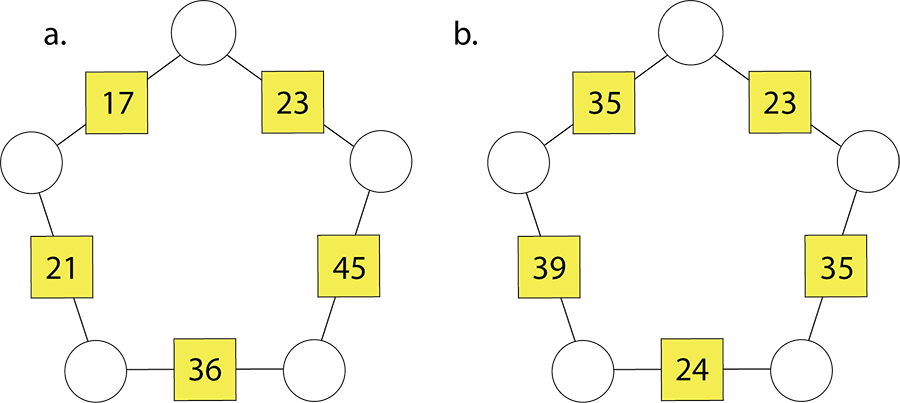
- Use an algebraic method to solve these pentagonal arithmagons:
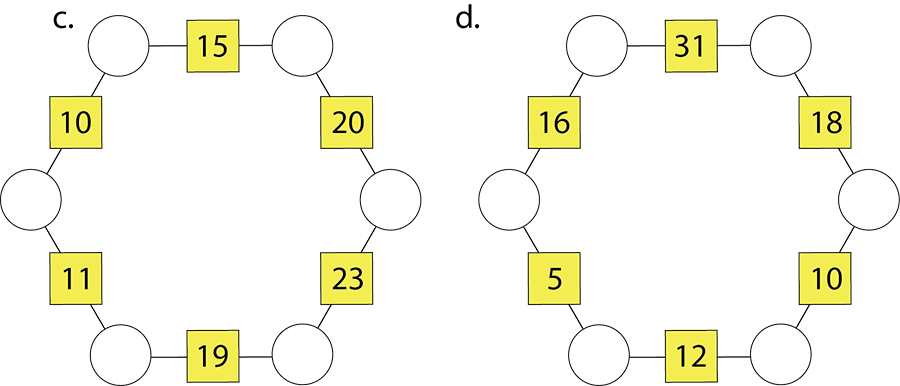
- Invent an algebraic way to solve these arithmagons:
Extensions
- The circle number method can be adapted to solve pentagonal arithmagons. Look at the diagram to work out how the method works.
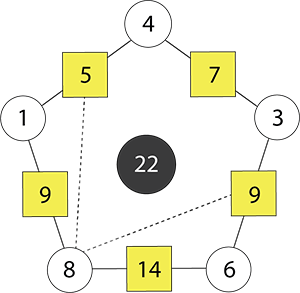
Use the middle number method to solve the pentagonal arithmagons above.
Prove how the method works using algebra. - Write and explain a rule to find the value of the circle number immediately ahead of the first box number in a sequence of box numbers, a, b, c, …, for a 7-sided (heptagonal) arithmagon, (Copymaster 5).
- Make a heptagonal arithmagon and check that your rule works.
- Make an octagonal arithmagon and check that your condition works.
- Make an octagonal arithmagon using (Copymaster 5).
- Make a poster, video, or digital presentation that can be used to explain and teach the concept of ‘arithmagons’ to other students.
Dear family and whānau
This week at school we have been investigating arithmagons. Arithmagons are polygons with a circle in each vertex, with a number inside each circle (circle numbers). Each side of the arithmagon includes a box with a number inside of it (box numbers). Each box number is the sum of the two circle numbers adjacent to it.
Ask your child to show you some examples of arithmagons we have worked with. Maybe you'd like to create some of your own!