Estimate and find percentages of whole number and decimal amounts.
Number Framework Stage 8.
Calculators.
Apparent contradictions can occur in percentage calculations when the percentages are calculated on the wrong quantity.
Using Number Properties
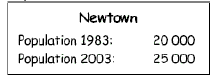
Problem: “Sally notices Newtown’s population has increased from 1983 to 2003. She claims the percentage increase is 25%. Samuel claims the increase is 20%. Explain how both can be correct.”
(Answer: Sally will argue the increase is 5 000 people.
Comparing this to the 1983 population, this is a fractional increase of 5000/20000 = 0.25 = 25%. But Samuel will argue the increase is 5 000 people, and comparing this to the 2003 population, this is a fractional increase of 5000/25000 = 0.2 = 20%. Both points of view are valid.)
Problem: “Harry buys cans of baked beans from the wholesaler to sell at his dairy. The wholesaler’s card says that Harry will make 35% profit. Harry calculates 1.35 x 1.30 and gets 1.755 not 2.00. Explain what is going wrong.”
(Answer: This is tricky. The wholesaler reasonably argues that Harry should be interested in profit as 35% of the money he gets in his till, not the amount he paid for the baked beans. So the 35% profit refers to a percentage of selling price not cost price.)
“Check that the wholesaler is correct.”
(Answer: 0.65 x $2.00 = $1.30 is correct.)
Problem: “Harry buys packets of chocolate biscuits at the wholesaler for $1.95 each. He wants to makes 35% profit on the selling price. What should Harry charge for a packet of biscuits at his shop?”
Discuss how to build up the flow chart and why Harry should charge 1.95 ÷ 0.65 = $3.00 for a packet of biscuits.
(Answer: 35% of the unknown selling price that needs to be multiplied is gross profit, so 65% of this price must be used to pay the wholesaler. The flow chart shows ? x 0.65 = $1.95. So, reversing the flow chart, the selling price of a packet of biscuits is 1.95 ÷ 0.65 = $3.00.)
Examples: Worksheet (Material Master 8–33).
Understanding Number Properties:
Harry decides to make the mark-up 40% on the selling price of the goods at his store. Make up a problem with this new mark-up and solve it.